DETERMINANTES

• Chama-se determinante da matriz quadrada $A$ de ordem $n$, e se indica por $\det A$, o número obtido a partir de operações entre os elementos de $A$.
• Representamos o determinante de uma matriz $A$ entre duas barras verticais $\vert A \vert$, que não têm o significado de módulo.
• Determinante de 1ª Ordem
$$A = [a_{11}] \Rightarrow |a_{11}| \Rightarrow \det A = a_{11}$$
• Determinante de 2ª Ordem
$$A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}$$ $$\Downarrow$$

$$\Downarrow$$ $$\det A = a_{11} \cdot a_{22} - a_{12} \cdot a_{21}$$
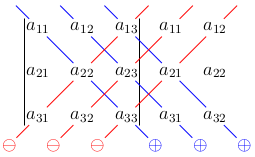
• Determinante de 3ª Ordem
$$A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}$$ $$ \Downarrow$$

$$\Downarrow$$ $\det A = a_{11} \cdot a_{22} \cdot a_{33} + a_{12} \cdot a_{23} \cdot a_{31} + a_{13} \cdot a_{21} \cdot a_{32} - a_{13} \cdot a_{22} \cdot a_{31} - a_{11} \cdot a_{23} \cdot a_{32} - a_{12} \cdot a_{21} \cdot a_{33}$
• Dada uma matriz quadrada $A = [a_{ij}]$ de ordem $n$, com $n \geqslant 2$, denominamos menor complementar relativo a um elemento $a_{ij}$ de $A$, e que se indica por $D_{ij}$, o determinante que se obtém quando se retira de $A$ a $i$-ésima linha e a $j$-ésima coluna.
• Dada uma matriz quadrada $A = [a_{ij}]$ de ordem $n$, com $n \geqslant 2$, denominamos cofator de $a_{ij}$, e que se indica por $c_{ij}$, o produto de $(-1)^{i + j}$ pelo menor complementar de $a_{ij}$, isto é: $c_{ij} = (-1)^{i + j} \cdot D_{ij}$.
• Considere a matriz quadrada $A = [a_{ij}]$ de ordem $n$, com $n \geqslant 2$, o determinante de $A$ é igual a soma dos produtos dos elementos de uma linha (ou coluna) qualquer pelos respectivos cofatores.
$$ A = \begin{bmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \\ \end{bmatrix}$$ $$ \Downarrow $$ $$\det A = a_{11} \cdot c_{11} + a_{12} \cdot c_{12} + \ldots + a_{1n} \cdot c_{1n}$$
• Propriedades dos Determinantes
• Casos em que um determinante é igual a zero.
• Quando uma matriz possui uma linha (ou coluna) nula.
$$\begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{vmatrix} = 0$$
• Quando uma matriz possui duas linhas (ou colunas) iguais.
$$\begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{i1} & a_{i2} & \ldots & a_{in} \\ a_{i1} & a_{i2} & \ldots & a_{in} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{vmatrix} = 0$$
• Quando uma matriz tem duas linhas (ou colunas) proporcionais.
$$\begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i1} & a_{i2} & \ldots & a_{in} \\ \lambda \cdot a_{i1} & \lambda \cdot a_{i2} & \ldots & \lambda \cdot a_{in} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{vmatrix} = 0$$
• Transformações que não alteram um determinante.
• Um determinante não se altera quando se trocam ordenadamente as linhas pelas colunas.
$$\begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{vmatrix} = \begin{vmatrix} a_{11} & a_{21} & \ldots & a_{n1} \\ a_{12} & a_{22} & \ldots & a_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \ldots & a_{nn} \end{vmatrix}$$
• Um determinante não se altera quando se somam aos elementos de uma linha (ou coluna) os correspondentes elementos de uma linha (ou coluna) paralela multiplicados por uma constante.
$$\begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{i1} & a_{i2} & \ldots & a_{in} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{vmatrix} = \begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{i1} + k \cdot a_{j1} & a_{i2} + k \cdot a_{j2} & \ldots & a_{in} + k \cdot a_{jn} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{vmatrix}$$
• Transformações que alteram um determinante.
• Um determinante muda de sinal quando se trocam as posições de duas linhas (ou colunas) paralelas.
$$\begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{vmatrix} = - \begin{vmatrix} a_{n1} & a_{n2} & \ldots & a_{nn} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{11} & a_{12} & \ldots & a_{1n} \end{vmatrix}$$
• Quando se multiplica uma linha (ou coluna) de um determinante por um número, o novo determinante fica multiplicado por esse número.
$$\begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & \vdots & \vdots \\ k \cdot a_{i1} & k \cdot a_{i2} & \ldots & k \cdot a_{in} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{vmatrix} = k \cdot \begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{i1} & a_{i2} & \ldots & a_{in} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{vmatrix}$$
• Escrevendo uma linha (ou coluna) de uma matriz como soma de duas parcelas, então o determinante dessa matriz pode ser obtido através da soma dos determinantes das duas matrizes obtidas da matriz original pela substituição daquela linha (ou coluna) pela primeira e pela segunda parcela respectivamente.
$$\begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{i1} + b_{i1} & a_{i2} + b_{i2} & \ldots & a_{in} + b_{in} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{vmatrix} = \begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{i1} & a_{i2} & \ldots & a_{in} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{vmatrix} + \begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & \vdots & \vdots \\ b_{i1} & b_{i2} & \ldots & b_{in} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{vmatrix}$$
• Propriedades Complementares.
• O determinante de uma matriz triangular superior (ou trinagular inferior) é igual ao produto dos elementos da diagonal principal.
$$\begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ 0 & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & a_{nn} \end{vmatrix} = a_{11} \cdot a_{22} \cdot \ldots \cdot a_{nn} = \begin{vmatrix} a_{11} & 0 & \ldots & 0 \\ a_{21} & a_{22} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{vmatrix}$$
• Se $A$ e $B$ são matrizes quadradas de mesma ordem, então $\det (A \cdot B) = \det A \cdot \det B$.
• Caso uma matriz quadrada $A$ seja multiplicada por um número real $k$, seu determinante passa a ser multiplicado por $k^{n}$, onde $n$ é a ordem da matriz, isto é: $\det (kA) = k^{n} \cdot \det A$.